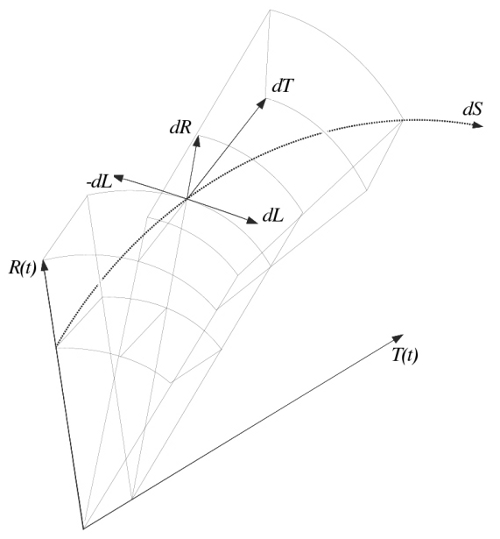
Fig. 1: R(t)=size of cosmological space, T(t)=clock-time of cosmological space, dR=change in size of cosmological space, dT=change in the rate of clock-time, dL=change in position of photon. The vector product, dR X dT = -dL

Trial and Error

Given three vectors: Cosmological Expansion, Speed of Light and Time, what field operations can one perform upon them? With respect to General Relativity, the Robertson-Walker Line Element, and the orbital motions of stars about galactic nuclei, I thought I would experiment with multiplication.

The expansion function, R(t) and the time function, T(t) are related here in that the cross product of their derivatives are constant and equal to the translation of light across a cosmological space under the influence of a distribution of gravitational energy that is being defined by the constructions in previous articles. The cross product has been chosen directly as an argument symmetrical to that of an electron moving in a magnetic field.
This article diagrams previously under-emphasized information, and a consequence of the “cosmological cross product”: that the photon moves across a space that contains no net gravitational energy, and so does no work on average. However, photons reaching the Earth from great distances have not average paths, but mostly histories of travel through”empty”, gravitationally positive—though increasingly weak—postive-gravitational space. In other words, excluding gravitationally lensed photons, observed photons from very deep space have not come under any significant gravitational influence of large concentrations of matter (galaxies), ie. about regions of galactic nuclei; though have traveled during a process of Universe expansion.

How the redshift of photons due to expansion, or due to time dilation escaping regions of negative gravitational energy (stars) relates to any “blueshift” that photons may obtain—caused by a path through a positive gravitational expansion—will hopefully be examined subsequently.