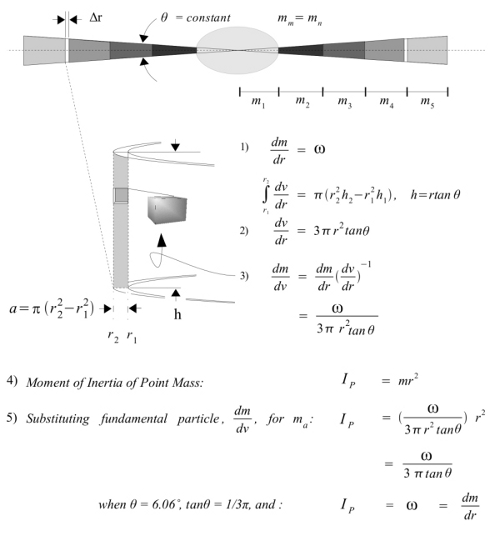
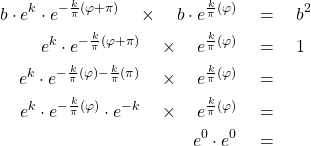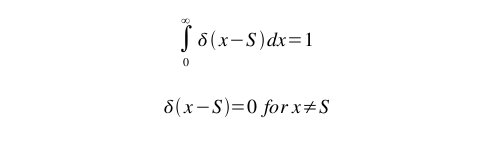The current range of estimates on the quantity of dark matter in the Universe often range from the mid- to upper-90s in percent.
At these quantities, under these large fractions of one, it would be equally plausible to assume that what is being observed (not being observed) is a presence so large that the number could effectively be 100% or inversely, zero (plus or minus three percent).
For example, adding all the matter in the Universe to equal in parts to some form of “dark-matter” would yield this result of zero (or inversely, 100).
It is supported by consensus that such quantities of anti-matter do not exist, and can not exist, in the Universe without interacting with matter and self-annihilating creating visible light and visible energy.
But in what other form could “anti-matter” be comprised?
Could there be a form of dark “anti-matter” that is non-interacting and repulsive of itself and all forms of matter, which is saturating every nominal volume of space unable to interact with any particle, even itself?
These questions are being answered in many ways, rightly or wrongly, using Sting Theory, MOND, and other ideas.
The motivations for these questions and answers are predicated by observations on the rotational dynamics of galaxies: Where they appear non-Keplerian, the gravitational attraction is presumed to be very small.
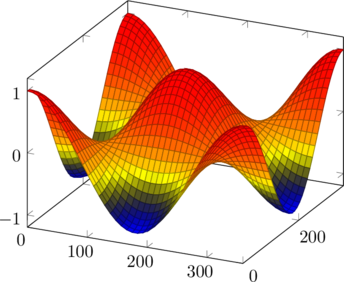
For example, in the image below[1], one can observe on the left-hand side an area where a “dip” emerges and then rises. This behavior is shared among many of the plots in the image and is indicating motion not consistent with Keplerian celestial orbits.

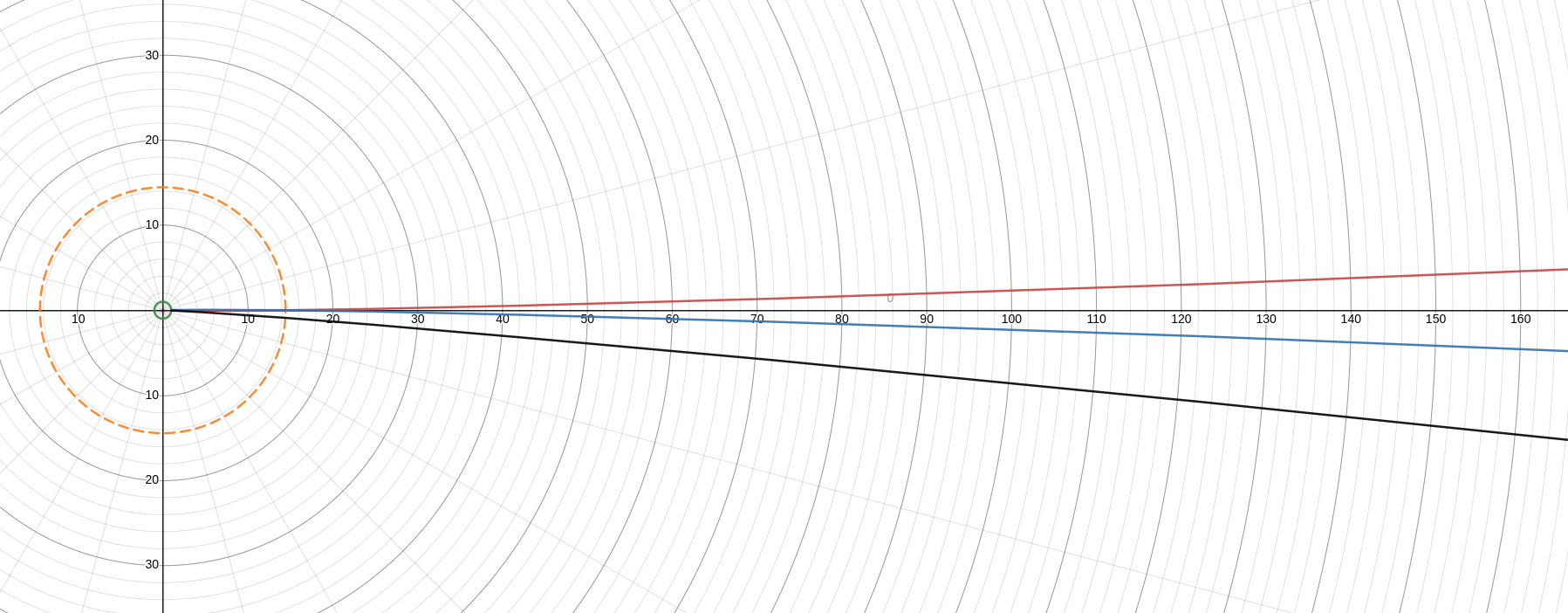
Below, one such area is approximated by shading in yellow within two curves. Similar curves are drawn using other values and colors:
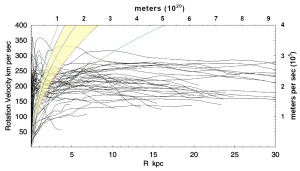
This family of lines are where the rotational velocity squared is divided by the radius and constant.
(1) ![]()
The yellow area is bounded by the violet curve on the left (b = 1.3 x 10-9 m/sec2), and by the red curve on the right (b = 6.4 x 10-10 m/sec2). This range of values for b is also highlighted with yellow in the table below.
The value of the green curve on the far left is 1.6 x 10-9 m/sec2. The value of the green curve on the far right, 3.2 x 10-10 m/sec2.
All the values of b are are within or near 10-9 to 10-10 in units of m/sec2.
This range, plus or minus two orders of magnitude (10-7– 10-12 ), is the region of study.
Perhaps certain units of acceleration are within the range of experimentation, given certain devices such as a very long pendulum, or other means.
| Color of Curve | b (m/sec2) |
| Green (left) | 1.6 x 10-9 |
| Violet | 1.3 x 10-9 |
| Blue | 1.0 x 10-9 |
| Red | 6.4 x 10-10 |
| Green (right) | 3.2 x 10-10 |
This website examines one special case, where the lower limit of the gravitational force exists and is within or around this range, such that:
1. All the forces of observable matter in the universe is equal to all the forces of an unobservable dark anti-matter type force, as described here.[1]
This dark anti-matter type force is repulsive and saturates every nominal volume of space equally. The quantity integrated across vast distances are significant and propel the expansion of the universe.
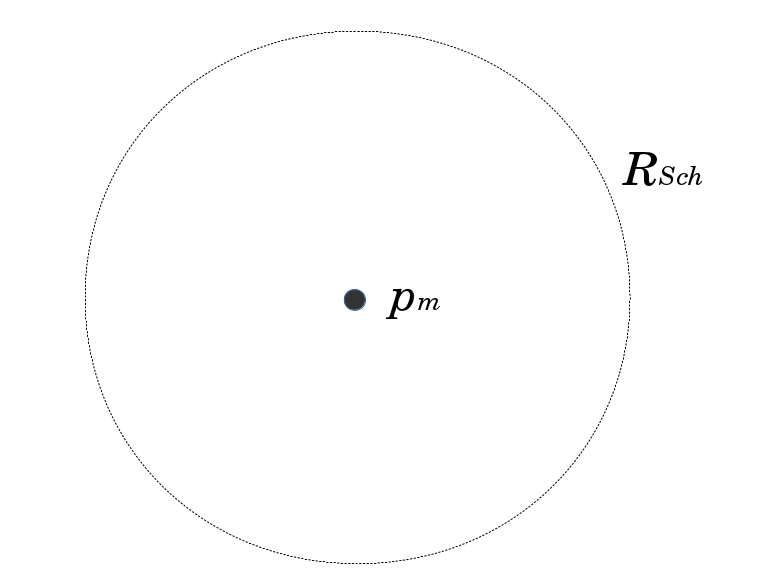
2. So that certain projection mathematics apply, there is an inverse-oriented surface at the limit of the Schwarzschild radius, as described here.[1][2]
DISCLAIMER: This assessment of the universe is not a consensus among any scientists that I know of. Anything claimed here is hypothetical.
Happy Pi Day, everyone!