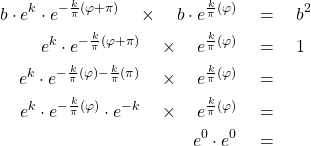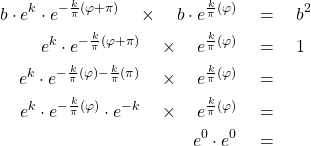There are some equations I’m working on.[1] They are intended to describe a projection from the outside surface of a sphere to the inside surface of a concentric spherical shell. This paradigm corresponds to a hypothetical gravitational field that has a net zero gravitational force in a universe with a single black hole.[2]
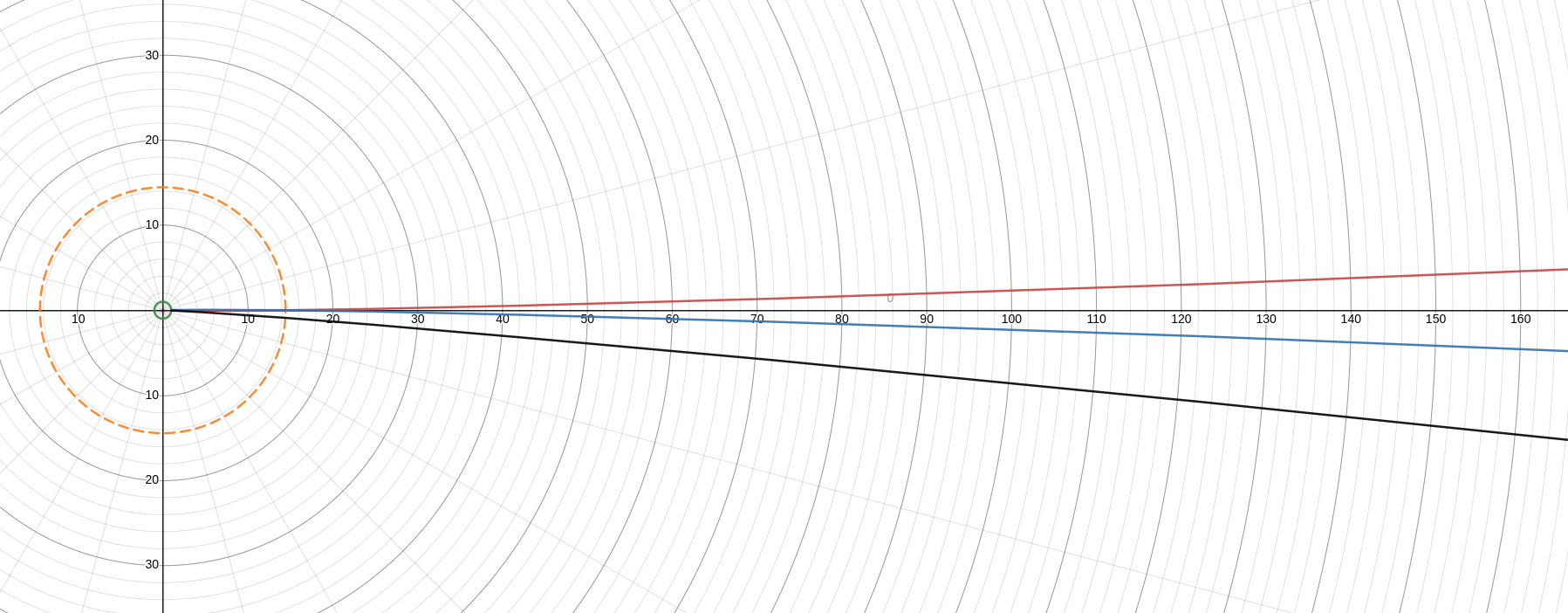
In two dimensions, the equations are scaled and rotated logarithmic spirals, which preserve the angles between its tangent and the intersecting circle — the polar slope angle is constant, which is consistent with flat planar projections. The equations in three dimensions will be published in a later post.

There exists at least one r1(φ1) and a scaled inverse r2(φ1 + φ2), where every product of r1(φ) with r2 (φ) is constant. See the proof at the bottom of the page.
See equations (1-5) below, which include:
(1) logarithmic spiral in polar form (red),
(2) the inverse of equation 1 (black),
(3) equation 2 scaled and rotated (blue), and
(4) domain, scaling and rotational factors.




(1) 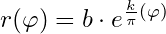
(2) 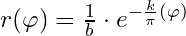
(3) 
(4) 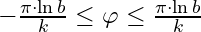
(5) 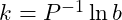
The variable P is the subtended projection angle in units of turns, 1=π (or 1=1/2 turn), and the variable b is the radius of the neutral surface, where all projection lines meet.
Below is an example drawn to represent the projection in three dimensions (not to scale) in a universe containing only a single black hole — a very small universe with a very large black hole!
[Click the image to enlarge.]

[1] For a more dynamic view of these equations, visit desmos.com.
[2] Here is where I am on all this speculation. Click the link to see a recently reported-measurable experiment inside (see page 18). This link has a graphic on page 24 that might be helpful.
Happy Pi Day, everyone!
PROOF: