CORRECTION: An earlier version of this post improperly converted radians to arcseconds, and some table entries were errors, among other errors. [July 28, 2022]
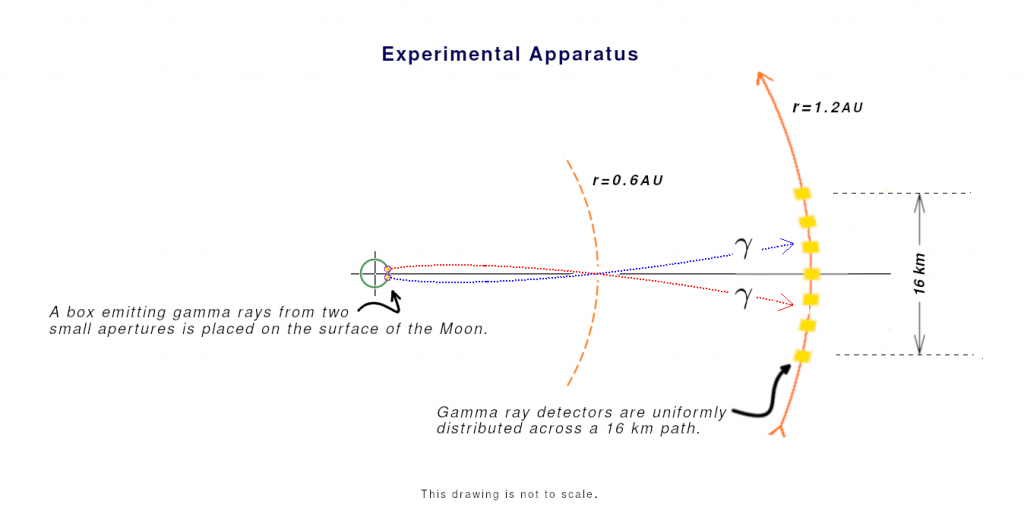
Calculations below provide a demonstration on how using the Rayleigh criterion (R = λ/D) may be used to distinguish between two sources of radiation emitted from the surface of the Moon. The two sources, which are emitted are: ● 0.11 mm apart ● viewed from a distance of 1.2 AU, and ● to be detected by a 16,000-meter detector.
According to the calculation, the radiation required for proper resolution would be gamma rays of wavelength 9.9 x 10-6 micrometers (3.0 x 1019 Hz) , or 124 keV.
The average distance to the Moon from Earth is 385,000 km (385,000,000 m). However, detectors must be farther than b Moon = 9 x 10 10 m (0.6 AU).
The distance b Moon is described in previous posts as a hypothetical spherical boundary (b) between which negative and positive gravitational accelerations are in the neighborhood of 10-10 m/sec2 and depend on the gravitational object’s Schwarzschild radius (a) and the radius of the observable universe (c), such that b2 = ac.
If detectors were placed 16,000 meters apart, located 1.8 x 1011 m (2 · b Moon = 1.2AU) from the gamma emission source on the Moon, and the image to resolve is 0.11 mm (1.1 x 10-4), then:
Tan-1 (1.1 x 10-4 m/1.8 x 1011 m) = 6.1 x 10-16 radians = 1.3 x 10-10 arcseconds
The Rayleigh criterion R (in arcseconds) = 0.21 λ/D, where λ is the wavelength in micrometres and D is the size of the telescope in metres, or the smallest distance between two gamma ray detectors.[1]
D = 16,000 meters *
R = 1.3 x 10-10 arcseconds
(1.3 x 10-10 x 16,000)/0.21 = 9.9 x 10-6 μm (gamma rays)
= 9.9 x 10-6 μm = 3.0 x 1019 Hz = 124 keV
*A 16,000 meter detector would be a very large. However, using a large number of smaller detectors spread across a 16,000-meter area and detecting a small fraction of the emissions may be sufficient to form a conclusion.
The resolution can be improved and the size D may be reduced, when used in conjunction with higher energy gamma rays, such as the decay of Technicium-99, which is used in nuclear medicine, has a half-life of six hours and produces 140 keV gamma rays, or Cobalt-60, which emits two gamma rays with energies of 1.17 and 1.33 MeV and has a half-life of 5.27 years.
Similar calculations can be made with respect to the Earth. Here are some preliminary Python scripts used to calculate the experimental parameters relative to the Moon and the Earth. The purpose of this experiment is to test orientability using gamma rays under extraordinary spatial constraints relative to a gravitational field.
Using a Box with Two Small Holes
For example, a box with two very small apertures containing Cobalt-60 emitting 1.1 – 1.3 MeV gamma rays is placed on the surface of the Moon (see image below). The center between the apertures lies on a plane perpendicular to the gravitational field. Emissions radiating from one of the holes would first have to pass through a filter, and the pair of emissions would be of different wavelengths and distinguishable from the point of view of the detectors.
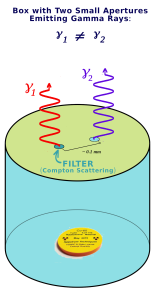
The entire speculation is, given high energy photons across large spatial distances, can orientability under the influence of a gravitational field be tested using the Rayleigh Criterion?
| Location | Distance between Apertures | Distance to Detectors | Required Energy of Gamma Rays |
| Moon | ~ 0.11 mm | ~ 1.2 AU | ~ 124 keV |
| Mars | ~ 0.9 mm | ~ 4 AU | ~ 54 keV |
| Earth | ~ 9 mm | ~ 13 AU | ~ 18 keV |
Click here to visit a site on gamma ray detection, NASA’s GLAST Burst Monitor. For a list of comparable scales, see this NASA planet distance chart.
