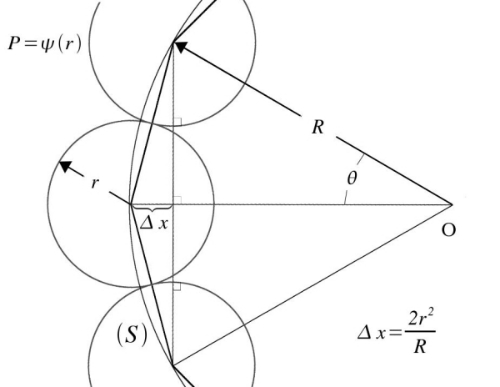
Fig 1: dx=2r2/R [proof]
Without hypothesizing on how such a classical state exists, a possible “confinement argument” is represented by this drawing that shows that for particles P, if they repel, work has to be performed across distance x to exist inside surface (S).
Resistance to compression is a quantum mechanical reaction that violates classical mechanics.
Because there are limits to the energy of “stationary” massive particles, as there are limits to the capacity for a particle to be stationary, defined by Plank’s Constant, I imagine a circumstance at the core of a collapsing neutron star, under such enormous compression at the core, that the capacity of a particle to remain confined at the very center is lost, and propelled outward, and unable to be replaced by another similar particle, for the very same reason, and as the remaining innermost shell of the core continues to be compressed by the increasing pressure of the collapse, a chain reaction ensues, and the star collapses simultaneously from both the outside inward and the inside outward.
How can I construct a plausible mathematical argument that would prove such a collapse takes place, if indeed it does?
Time delay in quantum coherence and tunneling?
Well, maybe in my dreams. The counter-arguments to hollow black holes would include statements to the effect that the particles would not all necessarily be fundamental particles, nor that are all of the same type; another counter-argument made might be that certain properties of the bodies to reach such a heightened state of entropy contradicts the possibility of such implicit order in its behavior (coherence). Or that the observed diameter of existing “black holes” and neutron stars, and the periods of their orbiting celestial objects, rule out their “hollowness.”
It would be possible that the theoretical fundamental particles in question, ie. those that comprise the entirety of the hypothetical surface, may be a particle that changes state with a period. For example, changing from having mass to not having mass, and these flavor changes corresponding to the period, may also correlate its position and direction relative to the surface and any coherence, or tunneling, across the interior of the sphere (or it’s surface): whether on the inside and moving toward the outside, or vice-versa.
Whether the shell of a “hollow black hole” could be high enough in its density to equal in mass a solid sphere of a similar diameter, ie. to within a few orders of magnitude— to within the resolving power of observations required to discriminate black hole from neutron star diameters, and how these diameters correspond to the periods of surrounding orbiting bodies.
Random notes’ quotes:
Einstein: from the point of view in General Relativity that one finds it “appropriate to introduce a tensor Tuv, ”[1] as “It is only the circumstance that we have no sufficient knowledge of the electromagnetic field of concentrated charges that compels us, provisionally, to leave undetermined in presenting the theory [GR], the true form of this tensor.”[2] And simultaneously, to “introduce a negative pressure for which there exists no physical justification.” [3] the “cosmological constant”.