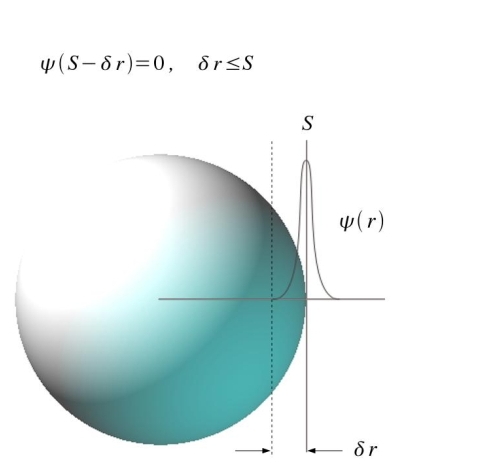
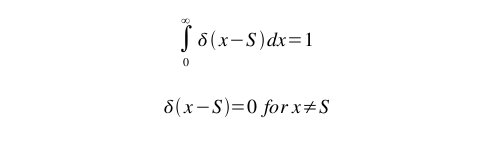Fig. 1: Minimum Conditions for Hollowness: (S) is the Shwarzschild radius, and the probability is zero that a mass particle can be found at the origin; another possibility is that the thickness of the surface (S) is very thin, and the probability is zero the particle will be found anywhere else but near (S).
Fig. 2: Gravitational Flux at the Gaussian Surface: If the thickness of the surface at (S) is very thin relative to the diameter at (S), (S) can be regarded “as practically flat.” [See Electromagnetic Fields and Waves (1979), by Vladimir Rojansky, p. 225.]
Fig 3: In other notation, Dirac’s Delta Function can be visualized as the limit of the function as the width of the curve shrinks to zero about (S). [See Electromagnetic Fields and Waves (1979), by Vladimir Rojansky, pp. 245-246.]
Why any of this may occur is not explained nor even successfully contemplated, although a good place to start seems Heisenberg’s Uncertainty Principle, the Schrodinger Wave Function, Special and General Relativity (where else is there??) and their confinement issues.
Consider the limits to the energies allowed in an amount of space, and the limits to the speed of communication; for example, an orbiting electron does not collide with a proton even though they are “very close” and their mutual attraction is extraordinary. The comparison of an electric field with a gravitational one, where the distribution of surface charge in a spherical conductor resembles the “surface mass” of a black hole would provide the added utility of precluding the black hole as a point-type singularity. It would be interesting to see under what conditions, if any, this “hollow” hypothesis can hold.
That all the gravitational flux may be limited in its transmission along the surface of a black hole, about the Schwarzschild radius, makes the relations of Equation (6) exact, and would describe the gravitational field of a black hole entirely, and is the subject of my study.