Is flat space a coincidence?

Is it possible that a Euclidean space is a requirement for the existence of observers? Is it an accident? And will all observers, past and present, always measure their observable space as Euclidean?

 

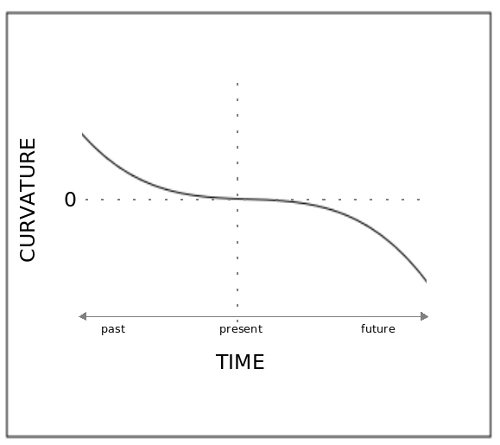
What I’ve been playing with is a problem outlined in the sketch “On a Dynamic Equilibrium for the Distribution of the Gravitational Force in Cosmological Space.”  The paper is a casual description of changing function values, and their derivatives, with respect to time. The essence of the paper is to fix the course of these function values to that of a negative gravitational force minimum, a null gravitational force, and a positive gravitational force maximum, over an average collection of bound galactic material in the cosmological space defined by the paper nicknamed Zero.

For no other reason than curiosity, the paper exploits a coincidence in the function under examination and constructs a representation in matrix form. It becomes evident that if the function values are to change as described in the paper—that the derivative of the gravitational force minimum increases as the derivative of the null gravitational force decreases—that the integral between these two points must also increase [image]. Yet it will be an assumption of the theory that this integral does not change, even as the function values and their derivatives do. The brief mention of the problem is at the bottom of page 4, highlighted in yellow.

 

If the integral would be made invariant, forced mathematically, with respect to time, by changing the function in no other way than a the change in the value of the exponent, the consequence would result in the relative flatness of one space-time to another. The interest in another paper, “Analysis and Computation”, will be in how this exponent, and the function values change continuously across time and how a theoretical observer in the present, measures the continually changing gravitational power of galactic nuclei across vast space-time distances.

Is it a coincidence that we exist in a locally flat space? Or does our space only appear locally flat—relatively flat to the past and the future?  Does this hold sway for all observers across all time scales?