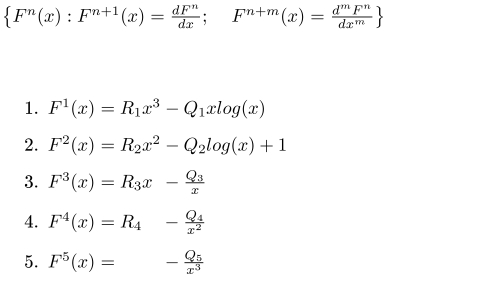Fig 1: Table of Derivatives

 

In the above example, P=1; signings and constants are assigned for simplicity. Note the continuity and discontinuity of the partial derivatives for a class C^k smooth function. I made a desmos graph of these functions here without variation in the coefficients.

The Unexplored Abstraction

A change from variable ‘x‘, to variable ‘r‘ in F⁴(x) to F⁴(r) yields a function in the form of an inverse square law of force with a positive constant, R₄.

A change from variable ‘x‘, to variable ‘t‘ in F³(x) to F³(t) yields a function whose shape is explored elsewhere and whose effects as a cross product with F⁴(r) are outlined in “Statement of the Problem” [See Article 4].  I ponder the meaning of this cross product of two functions of two variables, one the derivative of the other, one in time units, one in distance units and whether it is merely coincidental or meaningful to the changing structure of space-time.

F⁴ is the derivative of F³; and F³ is the derivative of F², F² is the proposed Universal Expansion function. F² is the derivative of F¹, and F⁵ is the derivative of F⁴. Curiously, the shape of F⁵ resembles a conservative field in 4-space, while the shape of F¹ invokes the exponential return of a system to equilibrium after a disturbance, sometimes written:

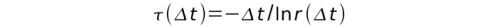
If the equations above were somehow representative of the dynamics of time and space vectors across cosmological time and distance scales, then how is this change in the “relaxation time” somehow representative of Universal Expansion, can this be useful? What would be the dimensional units, the numbers of dimensions? What is this Meta-Space-Time?

The Unconservative Gravitational Field.

In “Statement of the Problem” the product of F4(r) with F3(t) is defined as a vector field, a gravitational field, that changes with time in such a way that as t approaches infinity, ie. forever (the total life-time of the Universe), R4 approaches zero, and the field approaches a conservative field in 4-space.